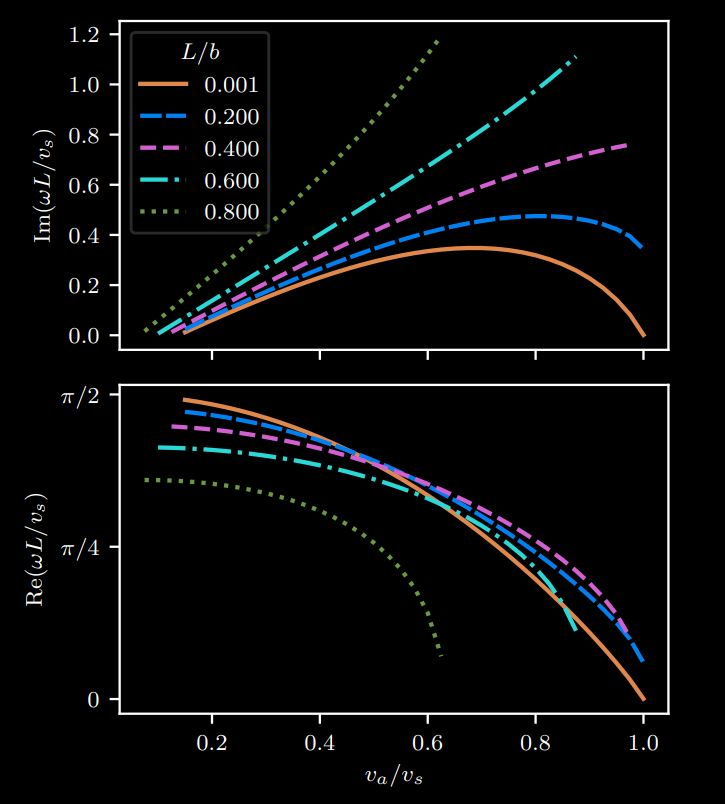
In very clean samples, electrons can flow like a liquid. For Farrell, Grisouard, Scaffidi (2021), I used a finite-volume method to simulate a viscous electron gas flowing radially in a ring. With certain boundary conditions, this setup experiences an instability: small perturbations to the steady state grow and oscillate at a certain frequency. Depending on the length of the channel, this frequency can reach the range of TeraHertz, a region of the electromagnetic spectrum for which few good sources or detectors currently exist!

The figure shows the instability’s growth rate and frequency as functions of the bias current in the radial direction.

The above movie gives the density profile (left panel) and momentum density (right panel) plotted over the length of the channel