Effective Theories for Dissipative Systems and Active Matter
- with Xiaoyang Huang, Isabella Zane, Aaron Friedman, Paolo Glorioso, and Prof. Andy Lucas
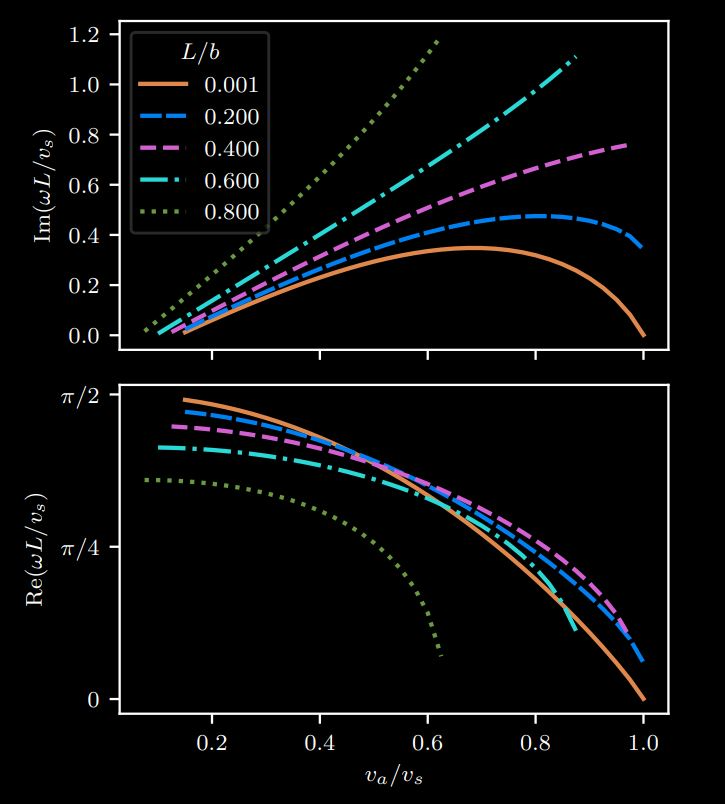
The Wilsonian paradigm of organizing phases of matter by the symmetries they obey (and break!) is a central tool for understanding equilibrium statistical physics. Can such a program exist for nonequilibrium systems as well? In Farrell, Huang, et al. (2023), we introduce an effective theory framework for dissipative classical systems both in and out of equilibrium, which describes stochastic dynamics in the presence of a thermal bath as well as nonthermal active matter. Rather than simply guessing stochastic equations, we derive them carefully based on symmetry principles. The most important symmetry is a generalized time-reversal symmetry, which is sensible even for active matter. Our formalism streamlines derivations of dissipative thermal dynamics such as Landau-Lifshitz-Gilbert spin dynamics or frictional rigid body rotation, and more importantly, it generates effective theories for active matter: non-reciprocal matter with predator-prey dynamics, active fluids and solids, and active phase separation. We hope that this approach facilitates a systematic investigation of the universality classes of active matter, and provides a common language for nonequilibrium many-body physics from high energy to condensed matter!
The figure shows how stationary thermal phases of matter and dynamic “active” phases of matter are controlled with different parameters inside our formalism.
Helical Hydrodynamics
- with Xiaoyang Huang and Prof. Andy Lucas
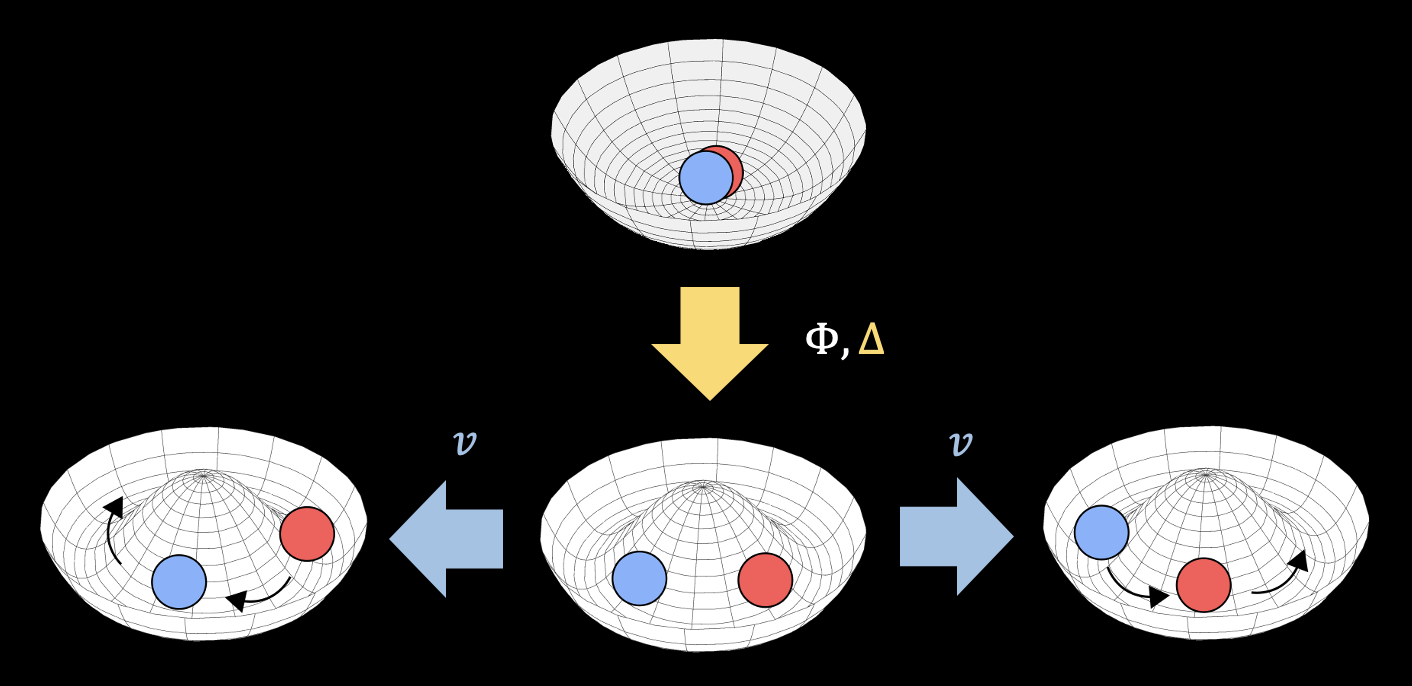
Normal fluids like water and air are described by the famous Navier-Stokes Equations, which apply to any system that respects Galileo symmetry. However, when the symmetry group is more exotic, novel terms may modify the NS equations and lead to interesting behaviour. For Farrell, Huang, Lucas (2022), we investigated a fluid with the symmetry of a helix: only the combination $\ P_z + L_z/\xi\ $ is a conserved quantity, not $\ P_z$ or $\ L_z \ $ separately. Interestingly, the transport coefficients of the helical theory are partially fixed by symmetry alone, and the fluid also features transverse responses, for example supplying a torque in the presence of a uniform electric field!
The figure is a cartoon illustrating helical symmetry.
Dyakonov-Shur Instability in an Annulus
- with Prof. Thomas Scaffidi & Prof. Nicolas Grisouard
- Supported by an NSERC Undergraduate Student Research Award
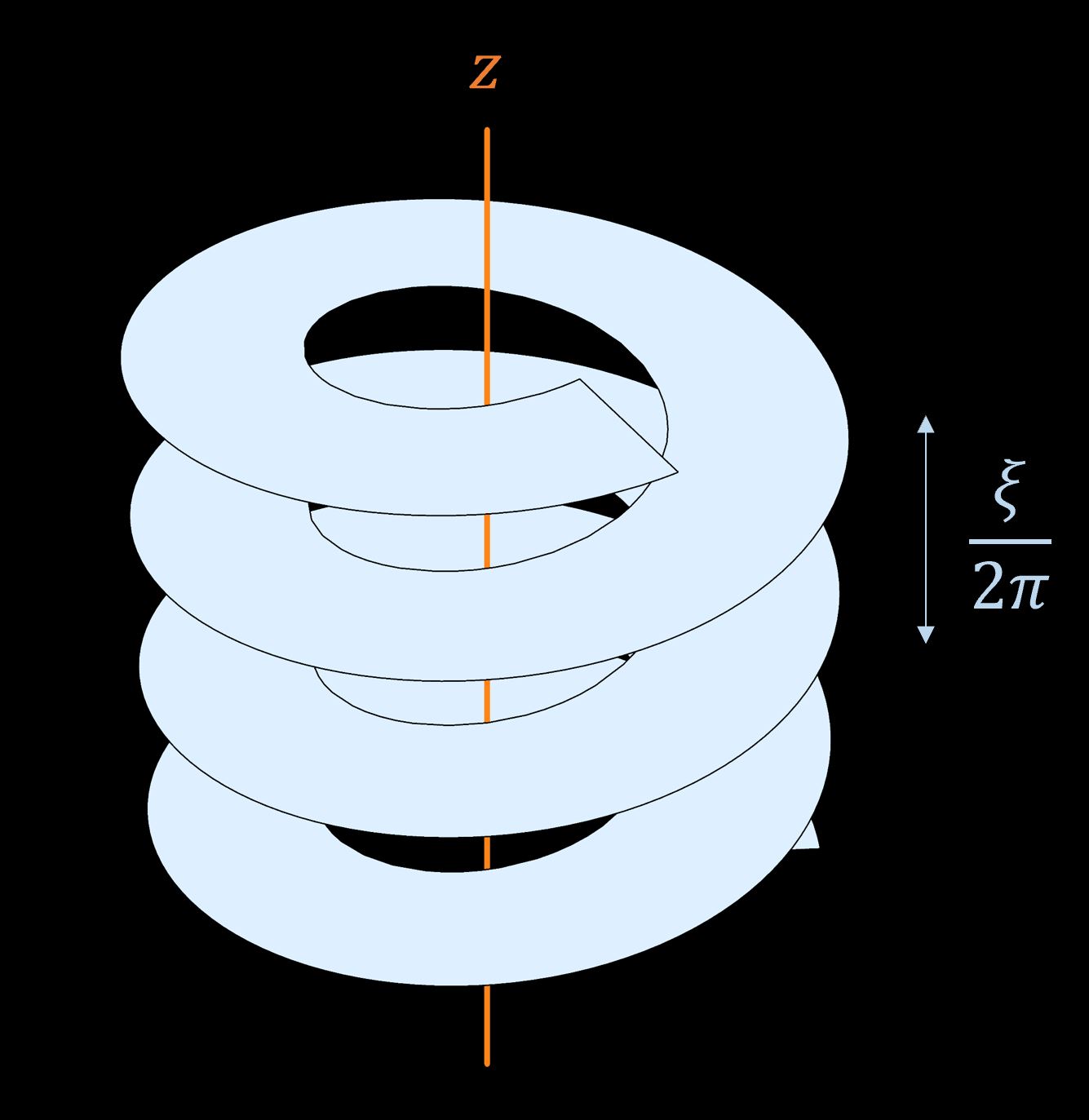
In very clean samples, electrons can flow like a liquid. For Farrell, Grisouard, Scaffidi (2021), I used a finite-volume method to simulate a viscous electron gas flowing radially in a ring. With certain boundary conditions, this setup experiences an instability: small perturbations to the steady state grow and oscillate at a certain frequency. Depending on the length of the channel, this frequency can reach the range of TeraHertz, a region of the electromagnetic spectrum for which few good sources or detectors currently exist!
The figure shows the instability’s growth rate and frequency as functions of the bias current in the radial direction.